Interpreting aggregated National Standards data: a thought experiment

Recently, there has been some public debate about the 2012 National Standards results, how these stack up against the results from 2011, and what they mean. But interpreting National Standards results is difficult and the debate sometimes lacks depth.

The following thought experiment seeks to illustrate one of the many reasons that we need to be careful before we leap to conclusions when interpreting the National standards results. As it is part of a thought experiment, the illustration is idealised. However, the numerical data informing it is self-consistent and the illustration itself does apply directly to recent public debate. This thought experiment is framed in terms of maths achievement, but it applies equally to reading or writing.

Suppose that we want to compare the changes in maths achievement of two populations of students that have occurred over the last year. To do this we need:

1.      To specify the two populations of students.

2.      To specify how we describe maths achievement.

3.      Two sets of maths achievement results for each population. One set of results is from last year and the other set is from this year.

In reality, Step 1 is not as straightforward as it might seem. For example, in New Zealand/Aotearoa we often report summary statistics that compare the maths achievement of Pasifika students with those of other students. But determining which students are counted as 'Pasifika' is a statistically and politically subtle and complex issue. However, since this is a thought experiment, we'll assume that we can complete Step 1 satisfactorily. We'll call our two populations of students Triangles and Diamonds.

Step 2 is also far from straightforward. Describing maths achievement in a way that is consistent, meaningful, beneficial, and useful for students, teachers, parents, principals, policy-makers and taxpayers is a monumental task. Since this is a thought experiment though, let's say that student maths achievement can either be described as 'below' standard or 'above' standard. We'll return to this point later as it is key to our thought experiment.

Step 3, as you might now expect, isn't at all easy. Many, many person-hours are spent creating, collecting and summarising student achievement data. For the purposes of our thought experiment though, we're free to make some results up. Here are some:

Table 1 Change in percent 'at' the standard

What do these results tell us? Both the Triangles and the Diamonds have improved over the year. The Triangles have improved 6 percentage points, from 93% 'above' standard last year to 99% 'above' standard this year. But the Diamonds have improved a whopping 38 percentage points from 31% 'above' standard last year to 69% 'above' standard this year.

Clearly, the Diamonds have improved more than the Triangles.

Or have they?

Let’s go back to Step 2 where we specified how we were going to describe maths achievement. Suppose that we could specify that maths achievement would be described in two ways. One way of describing student maths achievement would be exactly as we have done where students achieve either 'below' standard or 'above' standard. The other way would be to use a measurement scale where students achieve a score on a continuous scale. In our thought experiment, let's suppose that this scale runs from 0 to 40.

Is it okay to measure maths achievement in two ways? Sure. All it means is that somewhere on the measurement scale is a point called the 'below'/'above' boundary. Students who score below this point are described as 'below' standard. Students who score at or above it are described as 'above' standard. For our thought experiment, let's suppose the 'below'/'above' boundary occurs at 18 scale score points on our maths achievement scale and that this doesn't change from year to year.

When describing student achievement using a measurement scale we can report mean scores for the populations of interest. Here are the results for our thought experiment:

Table 2 Change in mean score

What do these results tell us? On average, both the Triangles and the Diamonds have improved over the year. The Triangles have improved by 4 scale score points, from 24 scale score points last year to 28 scale score points this year. The Diamonds have also improved by 4 scale score points, from 16 scale score points last year to 20 scale score points this year.

It is clear that on average, the Triangles and the Diamonds have improved equally.

But here's where it gets interesting: the results in Table 1 and Table 2 describe exactly the same changes in maths achievement.

How is this possible?

The short answer is that in the data summarised in Table 1 and Table 2, a greater percentage of Diamonds are clustered around the 'below'/'above' boundary than Triangles. So although the average scores of both populations improve by the same amount, a greater proportion of Diamonds cross the 'below'/'above' boundary than Triangles. The following graphs show this.

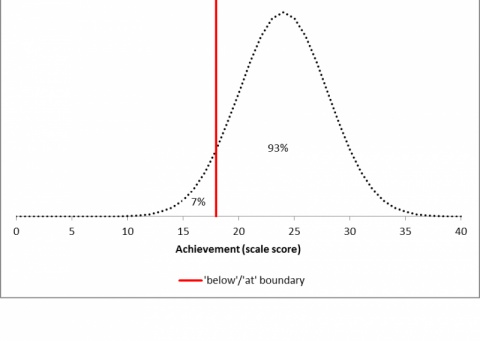
Figure 1 Triangle achievement last year

In Figure 1 we see that last year, only 7% of the Triangles were 'below' standard and 93% were 'above' standard. This means only 7% of the Diamonds are positioned to  improve from 'below'  to 'above'. The other 93% are already classed as 'above' and any improvement will still see them classed as 'above'. Last year's average score for the Triangles lies below the peak of the distribution - this corresponds to 24 scale score points.

Figure 2 Triangle achievement this year

In Figure 2 we see the result of the Triangles improving, on average, by 4 scale score points over the last year. Now only 1% of the Triangles are 'below' standard and 99% are 'above' standard. Overall, the percentage of Triangles achieving 'above' the standard has improved by 6 percentage points. This year's average score for the Triangles lies below the peak of the distribution - this corresponds to 28 scale score points.

In both Figure 1 and Figure 2 we see that only a small percentage of the population of Triangles is clustered around the 'below'/'above' boundary.

Figure 3 Diamond achievement last year

In Figure 3 we see that last year, 69% of the Diamonds were 'below' standard and 31% were 'above' standard. This means 69% of the Diamonds are positioned to  improve from 'below'  to 'above'. The other 31% are already classed as 'above' and any improvement will still see them classed as 'above'. Last year's average score for the Triangles lies below the peak of the distribution - this corresponds to 16 scale score points.

Figure 4 Diamond achievement this year

In Figure 4 we see the result of the Diamonds improving, on average, by 4 scale score points over the last year. Now 31% of the Diamonds are 'below' standard and 69% are 'above' standard. Overall, the percentage of Diamonds achieving 'above' the standard has improved by 38 percentage points. This year's average score for the Triangles lies below the peak of the distribution - this corresponds to 20 scale score points.

In both Figure 3 and Figure 4 we see that a large percentage of the population of Diamonds is clustered around the 'below'/'above' boundary. This is in contrast to the situation for the population of Triangles depicted in Figure 1 and Figure 2.

What this thought experiment shows is that how we describe student achievement effects how we quantify the change that has occurred.

When we compare the change in achievement between two populations using National Standards results, we don't have a measurement scale to rely on. We can only use changes in the percentage of students achieving 'above' the standard. But as our thought experiment demonstrates, we should be aware that although the percentage of students 'above' the standard can change quite differently for different populations, this doesn't necessarily mean that one population has improved more than another.